Pinball info
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Flip Out London - Thursday night league
- Thread starter Matt Vince
- Start date
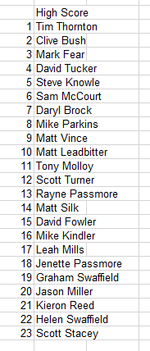
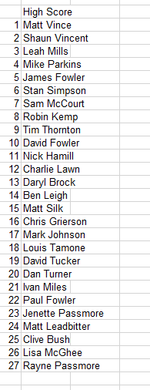
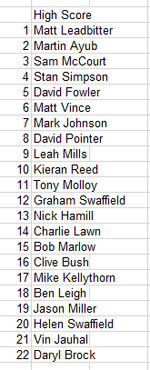
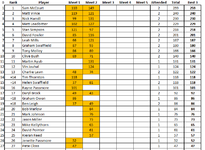
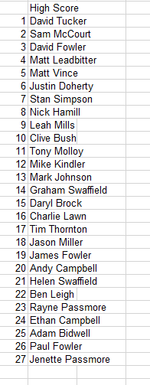
My first Thursday meet there too. Had a great laugh even if I came last on the High score comp. Well done Tim for showing us how to play Junkyard. Hopefully back next week then Pinfest! Hurrahhh!!!
That was a one off (well two) believe me. I usually play terribly on JunkYard!
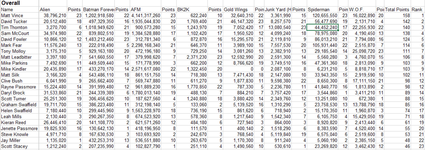
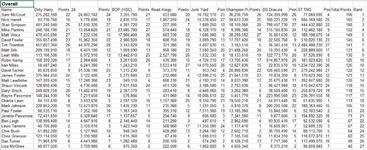
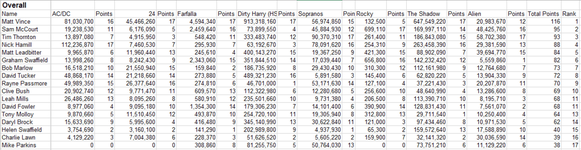
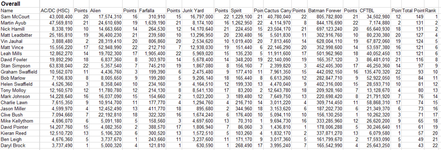
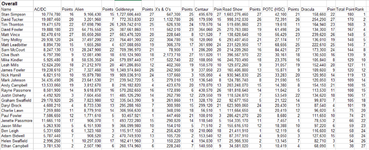
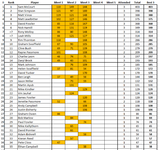
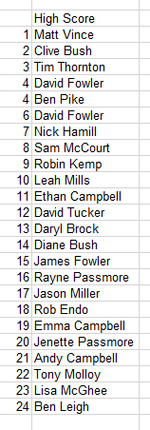
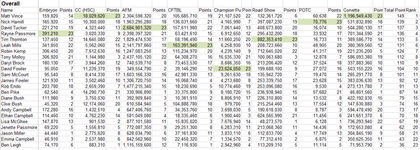
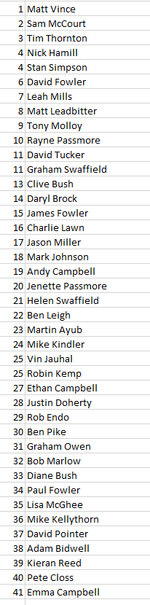
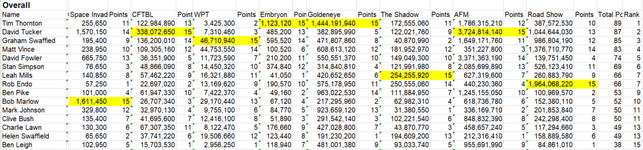
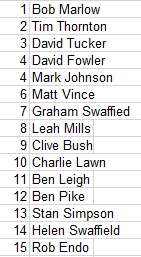
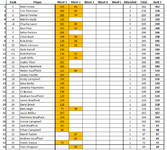
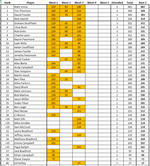
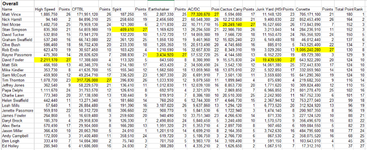
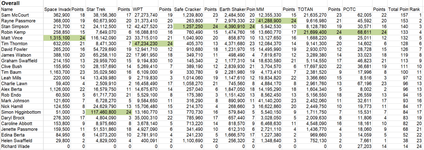
Great work by David F on cactus Canyon, taking 4th and 6th!
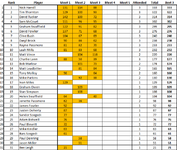
like the high lights